 Evolution
Evolution
 Life Sciences
Life Sciences
BIO-Complexity Paper Shows Many Multi-Mutation Features Unlikely to Evolve in History of the Earth
Doug Axe of Biologic Institute has a new peer-reviewed scientific paper in the journal BIO-Complexity titled “The Limits of Complex Adaptation: An Analysis Based on a Simple Model of Structured Bacterial Populations.” The purpose of this paper is to mathematically determine just how long it takes to evolve traits that require multiple mutations before any adaptive benefit is conferred on the organism.
To put this question in context, the ability of Darwinian evolution to produce features that require multiple mutations before gaining a benefit has been an issue long-debated between proponents of intelligent design (ID) and proponents of neo-Darwinism. In their 2004 peer-reviewed paper in the journal Protein Science, Michael Behe and David Snoke simulated the evolution of protein-protein interactions that required multiple amino acids. They found that for eukaryotic organisms, evolving a simple protein-protein interaction that requires two or more mutations might require more probabilistic resources (i.e. population sizes and numbers of generations) than would be generally available. This led to a spirited exchange in Protein Science among Behe, Snoke, and evolutionary biologist Michael Lynch. Another similar debate was spawned in 2008 when Rick Durrett and Deena Schmidt critiqued Behe’s arguments in The Edge of Evolution in the journal Genetics, which later brought a reply from Behe.
This latest paper from Axe responds to arguments from Michael Lynch and Adam Abegg, finding that they made a mistake–actually two mistakes–in their calculation of the length of time required for multiple mutations to occur when there is no adaptive benefit until all mutations are in place. As we’ve seen in many other areas, this is plain evidence of a legitimate scientific debate between ID proponents and proponents of neo-Darwinian evolution.
How Can Complex Adaptive Features Arise?
Axe opens his paper by explaining that it is becoming apparent that many complex biological features would require multiple genetic changes before any benefit exists. He writes:
Since we now have a large and rapidly growing catalog of functional protein systems that seem to be fundamentally complex, there is a growing sense that innovations of this kind would require complex adaptations, meaning adaptations needing not just one specific new mutation but several, with all intermediates being non-adaptive. If so, this may present a probabilistic challenge to the standard evolutionary model because it would require fortuitous convergence of multiple rare events in order for a selective benefit to be realized.
(Douglas D. Axe, “The Limits of Complex Adaptation: An Analysis Based on a Simple Model of Structured Bacterial Populations,” BIO-Complexity, Vol. 2010(4):1-10.)
He then notes that there are essentially three models that might be invoked to explain the origin of these complex features: molecular saltation, sequential fixation, and stochastic tunneling. In a section that I highly recommend to the reader, Axe lucidly explains the strengths and weaknesses of each model.
Regarding molecular saltation, he explains this is the “simplest” model as it merely entails “the de novo appearance in one organism of all necessary changes.” However, the downside for this explanation is that it requires “a very rare convergence of mutations” — so unlikely that biologists generally consider it “incompatible with Darwinian evolution.” In particular, Axe notes that the odds of all required mutations occurring in one single organism is proportional to ud, where u is the average specific base substitutions mutation rate per nucleotide site per cell, and d is the number of specific mutations required for a particular complex adaptive feature. Given the small size of mutation rates, the odds of such complex traits arising in one cell are exceedingly low. In the same way, the number of generations needed to produce the feature would be proportional to u-d. Again, given that mutation rates are very small, Axe notes that “u-d becomes exceedingly large” even for modest values of d, resulting in exceedingly long waiting times” for complex adaptive features. Thus, neo-Darwinists look for other mechanisms.
Regarding sequential fixation, Axe notes that in this explanation “point mutations become fixed successively,” but again, because we’re talking about traits where there is no advantage until all mutations exist, “these fixation events have to occur without the assistance of natural selection (or, in the case of maladaptive intermediates, even against natural selection),” making this explanation also “improbable.”
The primary model Axe tackles in his paper is stochastic tunneling, a model that is in a sense midway between the molecular saltation and sequential fixation models. According to Axe, stochastic tunneling “differs from sequential fixation only in that it depends on each successive point mutation appearing without the prior one having become fixed.” However, because the prior mutations are not yet fixed into the larger population, this means that the number of organisms that have the prior mutations may be small. Thus, this mechanism “must instead rely on the necessary mutations appearing within much smaller subpopulations,” or as Axe models it, bacterial lines. This model thus resembles molecular saltation in that it depends on all required mutations eventually appearing by chance– but anticipates this will happen after mutations are fixed in smaller subpopulations.
Axe explains why all of these models face unavoidable statistical improbabilities: “However, in view of the fact that the underlying limitation is an unavoidable aspect of statistics?that independent rare events only very rarely occur in combination?it seems certain that all chance-based mechanisms must encounter it.”
Finding Mistakes in Lynch and Abegg’s Calculations
Michael Lynch and Adam Abegg argued that stochastic tunneling can produce and fix a complex adaptive feature in u-1 generations rather than u-d generations. Intuitively, this doesn’t make sense because it ignores the necessary probabilistic resources that would be required to fix each additional mutation. Axe argues that their calculation is fundamentally wrong:
they find the waiting time for appearance and fixation of a complex adaptation requiring d base changes to scale as u-1 rather than the commonly assumed u-d. Because this should apply not only in the case of strict neutrality (which may seldom exist) but also in the more realistic case of approximate neutrality, and because it represents a striking departure from common probabilistic intuitions, it is important for this result to be examined carefully.
Axe’s paper then goes through a technical analysis of Lynch and Abegg’s calculation and finds that they made mistakes.
But if the implications of this equation are as implausible as has been argued, then there must be a mistake in the calculation.
This indeed appears to be the case. Specifically, of all the possible evolutionary paths a population can take, the analysis of Lynch and Abegg considers only those special paths that lead directly to the desired end?the complex adaptation. This is best illustrated with an example. Suppose a population carries an allele that confers no selective benefit in its current state (e.g., a pseudogene or a gene duplicate) but which would confer a benefit if it were to acquire five specific nucleotide changes relative to that initial state, which we will again refer to as stage 0. Lynch and Abegg assign a waiting time of (5u)-1 for a stage-1 allele to become fixed in this situation, which is valid only if we can safely assume that the population remains at stage 0 during this wait. But this cannot be assumed. A stage-0 allele of kilobase length, for example, would have about 200-fold more correct bases than incorrect ones (with respect to the complex adaptation), which means the rate of degradation (i.e., fixation of changes that make the complex adaptation more remote) would be about 600-fold higher than the rate of progression to stage 1. It is therefore very unlikely in such a case that the population will wait at stage 0 long enough to reach stage 1, and the situation becomes progressively worse as we consider higher stages.
He also finds they made a mistake in their calculations regarding stochastic tunneling:
Lynch and Abegg’s treatment of stochastic tunneling with neutral intermediates is also problematic. To derive an expression for the waiting time when the population is large enough to preclude fixation of intermediate stages, they approximate the frequency of stage-d alleles at t generations as (ut)d. While they note that this approximation is valid only if ut << 1, they overlook the fact that this restricts their analysis to exceedingly small values (ut)d. Specifically, they equate this term with the substantial allele frequency at which fixation becomes likely, and then proceed to solve for t, taking the result to be valid for arbitrarily large values of d. This leads them to the unexpected conclusion that “in very large populations with neutral intermediates, as d??, the time to establishment converges on the reciprocal of the per-site mutation rate, becoming independent of the number of mutations required for the adaptation”. But since they have in this way neglected the effect of d, it should be no surprise that they find d to have little effect.
Modeling Evolution
Having identified mistakes in the model of Lynch and Abegg, Axe presents his own analysis, aiming to accurately model the evolution of a multi-mutation feature. He models it in two cases: (1) when intermediate mutations are slightly disadvantageous, and (2) when intermediate mutations are selectively neutral. Axe seeks to give neo-Darwinian evolution a generous helping of probabilistic resources by modeling the evolution of bacteria — asexual organisms which reproduce quickly and have very large effective population sizes.
Unsurprisingly, Axe found that Darwinian evolution has great difficulty fixing multiple mutations when those mutations have negative selection coefficients (i.e. they are disadvantageous, or maladaptive). Neutral mutations have a better shot at becoming fixed, but even here Axe finds that the ability of neo-Darwinian evolution to produce multi-mutation features is highly limited.
The mathematics at this point admittedly become complex, but suffice to say Axe feels his results are promising because the solutions he presents for the two cases are consistent, which is a simple check that his work passes and Lynch and Abegg’s fails. Despite the complexity of the math, Axe’s paper summarizes his results in an easy-to-understand figure:
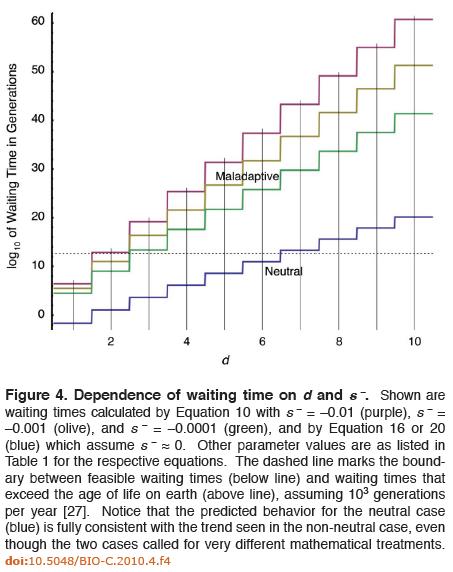
In the figure above, the x axis represents the number of mutations necessary for the trait to arise and confer some benefit to the organism. The y axis represents the base-10 logarithm of the number of generations required to fix the trait. Thus, if you’re at the coordinate x=2, y=10, then it would take the 1010 generations to fix a trait that requires 2 mutations before conferring any advantage. At point x = 3, y = 20, it would take 1020 generations to fix a trait that requires 3 mutations to provide a benefit. In this diagram, anything that requires a total number of generations above the dashed lines would exhaust the maximum number of probabilistic resources available for an evolving population of bacteria over the entire age of the earth.
The purple, olive, and green staircase lines represent various simulations of traits where intermediate mutations are maladaptive. In the green line, the selection coefficient of the mutations is said to be s = -0.0001; for the olive s = -0.001; for the purple s = -0.01. He found that at most only two slightly deleterious mutations could become fixed into a population of evolving bacteria. Axe’s model handles more highly maladaptive cases, but as can be seen from Fig 4, things get progressively worse as selection coefficients become more highly negative.
The blue line represents neutral evolution, where the selection coefficient of intermediate mutations is s = 0. In the case of neutral mutations, Darwinian processes have a better shot at fixing a few more DNA base substitutions, but even here the maximum possible number of mutations that can be fixed is probably only about six.
The Implications: Waiting for Multiple Mutations Just Got a Lot Harder
The implications of this analysis for Darwinian evolution are large and negative. As noted, Axe’s model made assumptions which were very generous towards Darwinian evolution. He assumed the existence of a huge population of asexually reproducing bacteria that could replicate quickly — perhaps nearly 3 times per day — over the course of billions of years. Yet even here, complex adaptations requiring up to six mutations with neutral intermediates can become fixed. Beyond that, things become implausible.
If only slightly maladaptive intermediate mutations are required for a complex adaptation, only a couple (at most two) mutations could be fixed. If highly maladaptive mutations are required, the trait will never appear. Axe discusses the implications of his work:
[T]he most significant implication comes not from how the two cases contrast but rather how they cohere?both showing severe limitations to complex adaptation. To appreciate this, consider the tremendous number of cells needed to achieve adaptations of such limited complexity. As a basis for calculation, we have assumed a bacterial population that maintained an effective size of 109 individuals through 103 generations each year for billions of years. This amounts to well over a billion trillion opportunities (in the form of individuals whose lines were not destined to expire imminently) for evolutionary experimentation. Yet what these enormous resources are expected to have accomplished, in terms of combined base changes, can be counted on the fingers.
He further concludes:
In the end, the conclusion that complex adaptations cannot be very complex without running into feasibility problems appears to be robust. … Although studies of this kind tend to be interpreted as supporting the Darwinian paradigm, the present study indicates otherwise, underscoring the importance of combining careful measurements with the appropriate population models.
Axe’s paper focuses on bacteria does not model the evolution of sexually reproducing organisms. But in sexually reproducing eukaryotic organisms, the longer generation times and lower effective population sizes would dramatically lower the number of mutations that could be fixed before acquiring some adaptive benefit. If we’re talking about vertebrates, the probabilistic resources available to Darwinian evolution would be much smaller than those available to bacteria, and the situation would be far worse.
