 Evolution
Evolution
 Intelligent Design
Intelligent Design
No, Avida Has Not Falsified Irreducible Complexity
The concept of irreducible complexity was introduced by Michael Behe in his book Darwin’s Black Box. He argued that certain molecular biological machines were:��������������������� ���������� �
composed of several well-matched, interacting parts that contribute to the basic function, wherein the removal of any one of the parts causes the system to effectively cease functioning.
 Such systems are irreducibly complex, and Behe argued that Darwinian evolution has a difficult time accounting for them. Many critics have insisted that evolution can produce irreducibly complex structures, pointing notably to the example of Avida, a computer model demonstrated in a 2003 Nature paper, "The Evolutionary Origin of Complex Features."Recently, I published an article in the journal BIO-Complexity, "Digital Irreducible Complexity," in which I argued that no computer model had successfully demonstrated the evolution of irreducible complexity.
Such systems are irreducibly complex, and Behe argued that Darwinian evolution has a difficult time accounting for them. Many critics have insisted that evolution can produce irreducibly complex structures, pointing notably to the example of Avida, a computer model demonstrated in a 2003 Nature paper, "The Evolutionary Origin of Complex Features."Recently, I published an article in the journal BIO-Complexity, "Digital Irreducible Complexity," in which I argued that no computer model had successfully demonstrated the evolution of irreducible complexity.
At the blog Panda’s Thumb, Richard B. Hoppe wrote a response, "Once again, desperately dissing Avida." He argues that I’ve made a number of errors in my description of Avida, and offers several objections to my thesis.
However, I believe that Hoppe is incorrect in his assessment. In some cases he has misunderstood what I intended to say. I have at some points been less clear than I should have been, and for that I apologize. In other cases Hoppe makes arguments irrelevant to the argument I presented.
Hoppe quotes my description of Avida’s EQU:
However, for the computer model Avida, the EQU function requires nineteen instructions, or separate steps.
He concludes:
Presented as it is in the Ewert paper, the implicit subtext is that there is but one specific program that can perform EQU, one ‘target’ for the digital critters.
Hoppe points out, accurately, that there are programs much longer than 19 instructions. However, the word "requires" in the above statement simply denotes the minimal number of instructions to compute EQU, as far as we know. It is not meant to claim all programs that compute EQU are exactly 19 instructions in length or that only one single program could compute EQU. This indeed could have been expressed more clearly in the paper.
Hoppe criticizes my brief discussion of the process of the evolution of EQU. However, that paragraph is not intended to be a precise technical description of Avida but rather to give a rough idea of the progress of evolution in it. It was intended to convey how the Avidan process of evolution starts without the computational instructions, and over time they are added by the evolutionary process. It was certainly not my intent to claim that Avida only used insertion mutations or that an individual instruction might perform a task.
Hoppe briefly mentions Minivida and indicates that he cannot find a visual depiction in it. I am not sure how he missed the visualization; perhaps there was a compatibility issue with his browser and the website . Nevertheless, here is a screenshot:
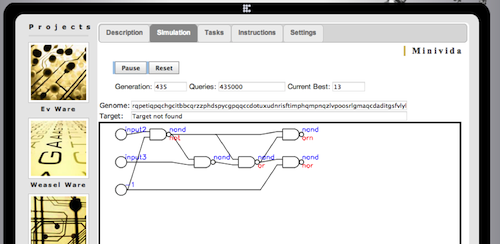
Hoppe quotes my paper, which points out that the paper in Nature made no claims to have evolved irreducible complexity. He writes that my statement is false:
In fact, that paper did show that irreducibly complex programs evolved, without specifically using Behe’s term.
There is a subtle but important difference between what I said and what Hoppe attempts to refute. I said that the paper did not claim to have evolved irreducible complexity. Hoppe replies that the paper shows the evolution of irreducible complexity. Evolving irreducibly complex programs and claiming to have evolved irreducibly complex programs are two different things. One can claim to have evolved irreducible complexity without having done so, and one can evolve irreducible complexity without claiming it as such. If a paper doesn’t even mention the term "irreducible complexity," it’s unlikely that it claims to have evolved irreducible complexity. Hoppe was arguing against a point different from the one I was making.
Nothing in the Nature paper indicates that it is intended to counter irreducible complexity. At the Kitzmiller v. Dover trial, Robert Pennock argued for the irreducible complexity of Avida programs. However, when asked whether that argument was in the Nature paper, he said:
It’s not. The Nature paper itself is meant just to be a test of a general evolutionary hypothesis, examining how it is that complex features arise. Darwin had specific things to say about that. What we were doing was simply looking into that, testing it in a way. It just turns out that it also applies to this case.
Hoppe dismisses my argument that irreducibly complex systems must be made of individually complex parts. However, he skips over the section of the paper where I defend the conclusion and he gives no reason to reject my reading of Behe. Instead, he merely accuses me of moving the goal posts. If this requirement is implicitly part of Behe’s conception of irreducible complexity (and I argue that it is), then I have not moved the goal posts. Rather, my paper attempts to clarify and quantify Behe’s original requirement.
An implication of my claim is that proteins are not irreducibly complex. Hoppe thinks I’m fighting this conclusion, but I’m not. I openly agree with it. Even without a minimal part complexity requirement, its difficult to see how a protein could be irreducibly complex. It would have to be shown that the removal of any of the amino acids in the protein would cause it to cease functioning. As far as I know, nobody has attempted to demonstrate such a thing.
Hoppe claims that Casey Luskin argues for the irreducible complexity of proteins, offering the following quote:
The specified complexity of proteins and protein-protein bonds are other examples [of irreducible complexity]. (Axe, 2000; Axe, 2004; Behe & Snoke, 2004)
However, if we look at the full passage from Luskin, without Hoppe’s bracketed addition, we find this:
Life exhibits both abstract language, signs, and symbols in order to produce self-replicating organisms. (Voie, 2006) Natural structures have been found that contain many parts arranged in intricate patterns that perform a specific function (e.g. complex and specified information), often taking the form of machines. The irreducibly complex molecular machine, the bacterial flagellum, is a prime example, as are some macromorphological structures. (Behe, 1996; Minnich & Meyer, 2004; Minnich, 2005; Becker & L�nnig, 2005) The simplest-known self-reproducing cell serves as another example. (Peterson & Fraser, 2001) The specified complexity of proteins and protein-protein bonds are other examples. (Axe, 2000; Axe, 2004; Behe & Snoke, 2004)
Hoppe asserts that Luskin thinks that the specified complexity of proteins is an example of irreducible complexity. However, within the context of the entire passage, the specified complexity of a protein, the simplest self-reproducing cell, and irreducibly complexity are all examples of "many parts arranged in intricate patterns that perform a specific function." Luskin isn’t saying that proteins are examples of irreducible complexity.
Hoppe makes the same claim about a quote from William Dembski, containing the critical sentence:
The problem of specified complexity thus arises not just at the level of irreducibly complex molecular machines but even at the level of the individual proteins that make up these machines and constitute their elemental constituents.
However, this isn’t saying that proteins are irreducibly complex, but rather that irreducibly complex molecular machines are made up of complex components. Dembski is saying exactly what I maintained in my paper: irreducibly complex structures are made up of complex elemental constituents.
Hoppe also quotes Tompkins and Woodmorappe, who do state that proteins can be irreducibly complex. But the critical question is what Behe intended, not how anyone else has used the term. Other have indeed written about "irreducible complexity" in a broader fashion than Behe. For example, many have argued for the irreducible complexity of the eye. However, Behe wrote:
we can’t yet evaluate the question of eye evolution (p 41, Darwin’s Black Box).
The question my paper was concerned with was Behe’s original definition, not the way in which others have broadened his definition.
In my paper I quoted Behe as criticizing an alleged evolutionary pathway by pointing to the complexity of the parts. Hoppe indicates that the website that I linked to in my paper was no longer available. The site is available now, and I can only assume that the problem Hoppe encountered was due to a temporary outage. Behe states that the hammer in a mousetrap has to be positioned at the edge of the platform, and Hoppe argues that this is unnecessary.
Baloney. That’s ludicrous. The hammer has to be "precisely at the edge of the platform"? Nope. Hammers that extend almost anywhere over the striking platform would do the job of killing mice.
Unfortunately, due to the website being unavailable, Hoppe could not know the context of Behe’s remarks. Behe is talking about a sequence of trap designs proposed by John McDonald. The particular design Behe is discussing does require the hammer to be precisely at the edge of the platform, as McDonald described it:
The next step is to remove the hold-down bar and bend the hammer so that one end is resting right at the edge of the platform, holding the hammer up in the cocked position. This is not as good a mousetrap as the four-part mousetrap. It is difficult to put the hammer exactly on the edge of the base, so a mouse-sized jiggle will cause it to snap.
Behe’s statement is correct in context. The particular trap design he was discussing does need the hammer to be positioned directly at the edge. That is an explicit requirement of the design as stated by McDonald.
In my paper, I develop a numerical requirement for the complexity of the individual parts of an irreducibly complex system. It is based on the probability of a system being produced by chance. Hoppe points out that I’ve not computed the probability of the entire system being produced by chance. This is true, but I also explained that I was only calculating the probability of a system with three components:
We are taking the cube root because we are assuming the minimal number of parts to be three. The actual system may have more parts, but we are interested in the level of complexity that would make it impossible to produce any system of several parts.
An Avida program is indeed too improbable to appear by chance in a regular run of Avida. But that’s not what I was calculating. Avida has many simple parts that add up to a large amount of complexity. But that’s not the same thing as having several individually complex parts, which I argued was a requirement of irreducible complexity.
Hoppe quotes my discussion of the probability, inserting the text in brackets:
The individual components should be improbable enough that the average guessing time exceeds these numbers. We can determine this probability [What probability? He just said he was estimating "average guessing time"!]
Given that the previous sentence refers to individual components being "improbable enough," I would have thought it was clear that I’m referring to the probability requirement for those parts; i.e., what probability is improbable enough. Additionally, I had previously discussed the relationship between probabilities and average guessing times:
Given a million attempts, we would expect to find a system with a probability of one in million once on average.
Hoppe states:
And what happened to Ewert’s "average guessing time"? It disappears after that one mention; time is not mentioned again. Again, I have no idea what it is supposed to be, if anything.�����������������������
This is simply false. The concept of average guessing time is developed in the previous paragraph. It is not just mentioned once and forgotten as Hoppe claims. The entire discussion of average guessing time is merely to motivate a particular complexity requirement; that is, a minimum probability for the individual parts of the system.
In my paper, I object to Avida on the grounds that it was designed to evolve. In response Hoppe writes:
Does Ewert imagine that in order to test a theory, one should ignore variables that the theory identifies as relevant?
No, a theory is free to postulate whatever background assumptions it deems necessary. But which theory is being tested here? The theory under question in my paper is irreducible complexity. The Nature paper was concerned with its own theory, but we are not concerned with the truth of that theory. We are concerned with the claim of irreducible complexity. This theory was developed by Behe, and he gets to define its background assumptions. It is not up to Hoppe or the authors of Avida to do that. You cannot declare irreducible complexity falsified if you have simply substituted you own assumptions for Behe’s.
Avida’s authors included precursor systems because their theory required it. But irreducible complexity questions the existence of such precursor systems. To test the theory of irreducible complexity you have to demonstrate the existence of such precursor systems, not simply assume it as Avida does.
In Climbing Mount Improbable, Richard Dawkins developed the metaphor of Mount Improbable. Evolution is only capable of climbing up gradual slopes. It cannot climb cliffs. What Avida demonstrates is that given a gradual slope, Darwinian processes are capable of climbing it. What irreducible complexity claims is that irreducible complex systems are surrounded on all sides by cliffs. Notice the distinction. Avida says that evolution can climb gradual slopes. Irreducible complexity claims that there are no gradual slopes. Avida is about what we can do with the gradual slopes, and irreducibly complexity is about whether or not the slopes exist. Avida provides no evidence that gradual slopes exist, it just assumes that they do. What Avida demonstrates is simply beside the point of the claim of irreducible complexity.
Irreducible complexity is not so much a claim about the abilities of the Darwinian processes as it is about the nature of the fitness landscapes that exist in the biological world. It is a claim that complex structures are surrounded by pits, labyrinths, and vast featureless plains. According to irreducible complexity the real fitness landscapes in biology are ill suited to Darwinian evolution. Avida shows that when the landscape is ideal for Darwinian evolution, evolution succeeds. That demonstrates nothing about irreducible complexity.
If you are content to test Darwinian evolution’s abilities under ideal circumstances, you may postulate whatever fitness landscape you want. However, if you want to know whether that ideal fitness landscape will be in place, you have to defend your fitness landscape. You can argue that your fitness landscape derives from biologically realistic assumptions. You can argue that it derives from the natural consequences of the problem space. However, it is not a defense to postulate a fitness landscape with certain properties just because successful evolution requires it. Whatever that is testing, it isn’t the nature of realistic fitness landscapes.
I wrote:
There is no attempt to show that the parts are necessary for the working of the system.
Hoppe objects, and he’s correct. I meant to write this:
There is no attempt to show that the roles of the parts are necessary for the working of the system.
That is in reference to my discussion of the requirement of identifying necessary roles.
Hoppe discussed two of my objections to Avida. I argue that Avida’s parts are too simple. He accuses me of moving the goal posts while not discussing my defense of the goal posts. He appeals to others who have argued for the irreducible complexity of proteins, which is only half-correct and irrelevant. He misunderstands the calculated limit. I further argued that Avida was designed to evolve. He objects that a theory is allowed to postulate what it wants; however, that’s irrelevant as the theory being tested is irreducible complexity. Irreducible complexity questions the existence of precursor systems; ergo simply postulating them as in the case of Avida demonstrates nothing.
Hoppe has legitimately pointed to flaws in my writing. However, as a critique of the argument presented in my work, Hoppe’s post falls flat. He misunderstands my text in subtle but crucial ways, objecting to statements I never intended to make. He offers arguments irrelevant to the questions at hand. The case in my paper still stands. Avida has not falsified irreducible complexity.
