Editor’s note: This is the third installment of a five-part series taking a closer look at Michael Behe’s arguments that polar bear genes experienced adaptive mutations that were damaging. Find the full seminar here.

In their second objection to Michael Behe’s case in Darwin Devolves, Nathan Lents and Arthur Hunt argue that Behe exaggerates the number of positively selected genes in polar bears that are estimated to have suffered at least one damaging mutation. Or to be more precise, they think Behe’s lower limit is overstated, while agreeing with his upper limit. Let’s evaluate their claims. Here’s what they write:

Now it’s getting harder to excuse Behe’s exaggeration. Specifically, using one specific predictive algorithm, the authors found that only 7 of the 17 genes with the strongest signatures for positive selection are unequivocally predicted to possess at least one “damaging” mutation. Even Behe’s “about half” is just 41%, which means that the lower limit on Behe’s estimation is also wrong. It’s not 65-83%, it’s 41-83%. The range is so wide because computational predictions invariably involve uncertainty.

It’s worth noting that they accept the PolyPhen-2 program used by Liu et al. (2014), recognizing it as capable of finding that a protein’s function was probably damaged by a mutation. This contradicts objections made by other critics of Behe, answered here in the preceding post. 

A Matter of Methodology

Now, everyone knows statistics are easily manipulated. What matters is whether the methodology behind the statistics is sound. Presumably, the closer your method is to that used by authorities published in peer-reviewed papers, the better. Much like we saw in considering the previous objection, Lents and Hunt in their own treatment of Darwin Devolves come up with different numbers from Behe only by using a different methodology than the one used by the paper itself. When you follow the methodology employed by Liu et al., you get numbers like what Behe provides in his book. 

As we saw, Liu et al. (2014) stated that a mutation was “predicted to be functionally damaging” if one of the two algorithms used by the PolyPhen-2 program found that it was either “possibly damaging” or “probably damaging.” (Again, finding a mutation was “possibly damaging” doesn’t mean the evidence is weak; the paper was simply being conservative in recognizing the potential for false positives.)

So how did Lents and Hunt come up with their numbers? As noted, their upper limit for the number of genes that experienced at least one damaging mutation (83 percent) was exactly the same number obtained by Behe. The math is easy to understand: Look at Table S7, reproduced in full below from Liu et al. (2014). Count the total number of genes where at least one mutation was predicted to be damaging (in this version of the table, a mutation is predicted to be damaging if it is shaded by any color). That number is 14. Divide 14 by the total number of different genes in the table, which is 17, and you get 82.3 percent. Now round up to 83 percent because we’re dealing with discrete entities and you can’t have only part of a discrete entity. The method used to generate this upper limit follows Liu et al., who considered a mutation as “predicted to be functionally damaging” if at least one algorithm found it was “possibly” or “probably” damaging. 

Cautious with Numbers

But Behe in his book was being cautious. He listed the upper limit of the number of genes experiencing damaging mutations. But he also sought to provide a lower limit by asking how many genes had a mutation where both algorithms predicted it was damaging (following, again, the methodology of the Liu et al. paper).

If you look at Table S7 below, you’ll see the pink or red shaded mutations are those where both algorithms predicted the mutation was damaging. In this case, 11 out of the 17 genes had at least one mutation where both algorithms used predicted it was damaging. Divide 11 by 17 and you get 64.7 percent, once more rounding up to 65 percent because we’re dealing with discrete entities. This is how Behe calculated his lower limit of 65 percent.

The full Table S7 from Liu et al. is shown below. The text of the table is unaltered but the shading has been added according to the following scheme:

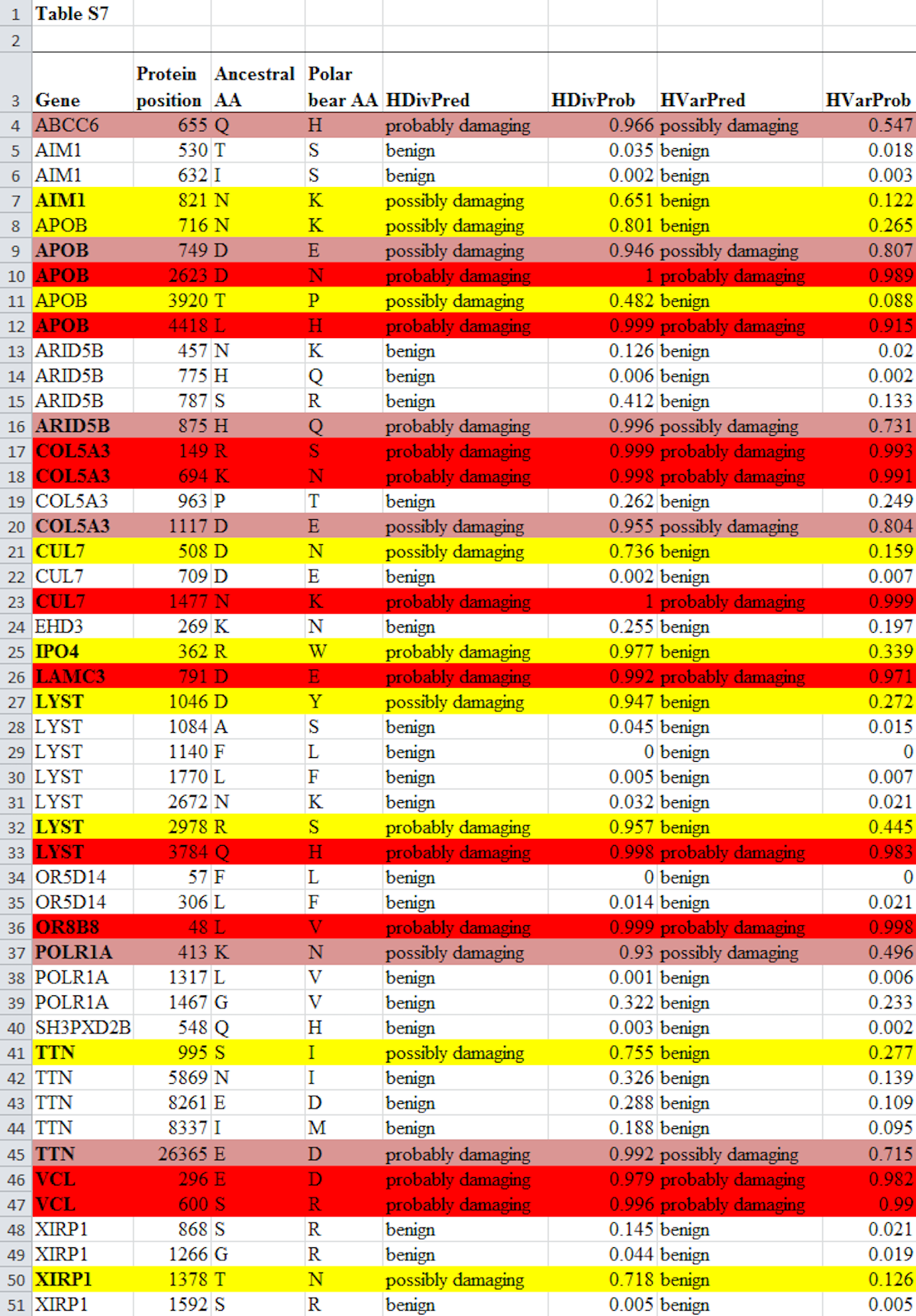
The critics focus on how to calculate the lower limit of the number of genes that experienced at least one degradative mutation. Hunt and Lents calculate a lower limit of 41 percent. They do so by claiming only 7 of the 17 genes had a mutation that caused damage. To get this result, they only counted cases where both algorithms predicted that the mutation was “probably damaging” (shaded yellow in the table above). These, they say, represent cases where, in their words, the paper “unequivocally predicted” that the mutation was damaging. They excluded from their lower estimate all cases where one, or both, of the algorithms predicted the mutation was “possibly damaging.” That’s one way to run the statistics, but it’s not at all like the methodology of the paper itself. The discrepancy in method is crucial to understanding this argument against Behe. Yet curiously, it is omitted from mention by Lents and Hunt. Why?

Following His Source

Unlike Lents and Hunt, Liu et al. considered a mutation to be “predicted to be functionally damaging” even if one of the two methodologies found it was “possibly damaging.” Again, recall that even in the “possibly damaging” cases, there was still good evidence that the mutation was damaging and it was only called “possibly damaging” out of concern for false positives. But even in these cases the evidence pointed to the mutation being damaging. Behe’s lower limit followed the paper’s methodology (a mutation was damaging if one algorithm found it was “possibly damaging”), whereas Lents and Hunt used a different methodology (a mutation was only damaging if both algorithms found it was “probably damaging”). 

Method, of course, is a valid subject for debate, and Lents and Hunt are welcome to make their case against the approach adopted by Liu et al. But obviously, Behe did nothing wrong in simply following the methodology of the paper he was citing. 

A major irony here is that of all of the numbers that have been calculated for the percentage of genes that probably experienced a damaging mutation, the one that most closely follows the paper’s methodology is the upper limit, first calculated by Behe and agreed upon by Lents and Hunt! When calculating this percentage, any mutation that was found by at least one algorithm to be “possibly” or “probably” damaging is said to represent a mutation that is “predicted to be functionally damaging.” That’s the exact methodology followed by the paper, so Behe’s upper limit of 83 percent of genes arguably stands as the best estimate of the number of genes experiencing at least one damaging mutation. 

In any case, it’s clear that Behe’s estimate of the percentages of genes that underwent damaging mutations is no “exaggeration” but is in fact exactly what one would expect from any scientist following Liu et al.

Inconsistent and Unreasonable Standards

There’s a further irony: The argument here by Lents and Hunts, call it objection (2), leads to a result that absolutely refutes their other complaint, objection (1), discussed in the earlier post, namely that “There is no evidence for Behe’s claim that APOB is degraded or diminished in polar bears.”

In objection (2), Lents and Hunt state that when both algorithms predict that a mutation is “probably damaging,” this means the gene in question is “unequivocally predicted to possess at least one ‘damaging’ mutation.” Those are their words. Liu et al. didn’t apply such a standard, but if that’s how they want to argue, it’s their prerogative. But notice the result. 

Two of the mutations studied in the paper that meet their standard of “unequivocally predicted” to be damaging are mutations in the gene APOB (at positions 2623 and 4418)! Not only that, but one of those two mutations (position 2623) got the highest possible score from the algorithm (1.0) for predicting a damaging effect. Yet Lents and Hunt made the strongest possible claim against that mutation being damaging, saying there was “no evidence” that APOB had experienced damaging mutations: 

• “There is no evidence for Behe’s claim that APOB is degraded or diminished in polar bears”
• “Clearly, the authors do not expect the polar bear APOB to be broken or damaged”

Do you see the problem? By their own standards, they admit that APOB has two mutations that are “unequivocally predicted” to be damaging. This means APOB is “unequivocally predicted to possess at least one ‘damaging’ mutation.’” Yet they say, “There is no evidence for Behe’s claim that APOB is degraded or diminished in polar bears.” They just provided the evidence that their first objection is wrong!

What’s really going on here is that Lents and Hunt are applying inconsistent and unreasonable standards in different situations, all designed not to uncover the truth but to impugn Behe:

• In objection (1), they apply a standard where EVEN IF both algorithms used in the study find that a mutation is predicted to be “probably damaging,” THEN Behe is NOT ALLOWED to say that there is evidence that the mutation is damaging. 
• In objection (2), they apply a standard where ONLY IF both algorithms used in the study find that a mutation is predicted to be “probably damaging,” THEN AND ONLY THEN is Behe ALLOWED to say that there is evidence that the mutation as damaging. 

The contradiction is obvious, and clearly it’s being employed to entrap Michael Behe. It is Behe who is consistent with Liu et al. and he comes up with logical, predictable results. Critics have insisted that Behe should retract his case, and Nathan Lents and Arthur Hunt would appear to agree. That claim, as we are seeing, is completely unwarranted, as Behe’s arguments are fully justified in light of the authority, Liu et al. (2014), that he cites. But there is more to say on this subject.

Photo credit: Eva Blue via Unsplash.