 Evolution
Evolution
 Intelligent Design
Intelligent Design
Fingerprints of an Intelligent Programmer: The “Entropy = Information” Mistake

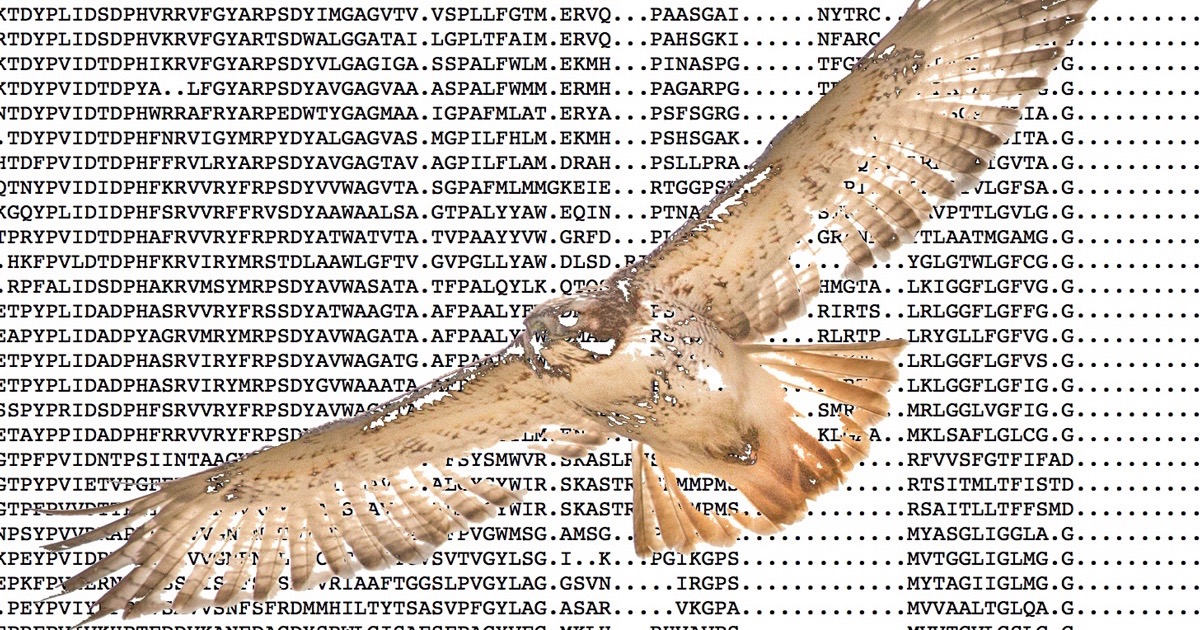
Highly significant levels of functional information encoded within the genomes of life provides strong evidence that the digital software1 we observe within the DNA of all plants and animals came from an intelligent programmer.
Note that this is not an argument based on ignorance — “We don’t know what can write computer code, therefore God did it.” Quite the contrary; it is based on the observation that intelligent minds can write digital software. It follows from this that a highly probable candidate for the functional information encoded in DNA is an intelligent mind.
This scientific observation raises philosophical implications that some scientists resist — not on any scientific basis but for philosophical reasons. The first mistake made by some scientists is the failure to distinguish between classical measures of information and the more recent concept of functional information. The second mistake they make is the belief that entropy = functional information.
First Mistake:
The first mistake is the failure to distinguish between classical forms of information versus functional information, and is described in a short 2003 Nature article by Jack Szostak.2 In the words of Szostak, classical information theory “does not consider the meaning of a message.” Furthermore, classical approaches, such as Kolmogorov complexity,3 “fail to account for the redundancy inherent in the fact that many related sequences are structurally and functionally equivalent.” It matters a great deal to biological life whether an amino acid sequence is functional or not. Life also depends upon the fact that numerous sequences can code for the same function, in order to increase functional survivability in the face of the inevitable steady stream of mutations. Consequently, Szostak suggested “a new measure of information — functional information.” In a subsequent, 2007 PNAS paper, Robert Hazen and colleagues, including Szostak,4 mathematically defined functional information as follows:
I(Ex) = -log2[M(Ex)/N] Equation (1)
where,
N = total number of possible configurations or sequences (both functional and non-functional),
M(Ex) = total number of configurations or sequences that satisfy the functional requirements,
I(Ex) = functional information (the number of bits necessary and sufficient to specify a given function).
For protein families, unfortunately, there are two unknowns, I(Ex) and M(Ex). That same year, my colleagues and I published a paper5 presenting a method to estimate I(Ex) for protein families, from which the probability M(Ex)/N could be estimated.
Example of first mistake: Let us assume that a compartment in a space station must be filled with carbon dioxide, which is placed in the compartment in its solid crystal state, a perfectly ordered, trigonal crystal structure. In that state, the thermodynamic entropy of the gases in the compartment would be at a minimum and the amount of information required to describe the position, momentum and energy of the carbon dioxide would be minimal. As the chunk of frozen carbon dioxide turned to a gas and filled the compartment, thermodynamic entropy would increase and the arrangement of molecules would become increasingly random. The information required to describe the entire set of carbon dioxide molecules, at any time t, would increase as thermodynamic entropy increased. One might mistakenly think, therefore, that increasing entropy = increasing information. The mistake is confusing between classical information and functional information, specifically, it is the failure to “account for the redundancy inherent in the fact that many related sequences are structurally and functionally equivalent.” To clarify, there is not just one, single distribution of carbon dioxide molecules that will serve the function of filling the compartment. As the thermodynamic entropy of the carbon dioxide in the compartment reached equilibrium, almost any arrangement of molecules would satisfy the function. As a result, M(Ex) ≈ N, and the amount of functional information required to satisfactorily fill the compartment with carbon dioxide would be very close to 0 bits. Also, the value of I(Ex) is a constant, regardless of the actual thermodynamic state of the carbon dioxide in the compartment. In other words, the actual thermodynamic entropy at any time t, has nothing to do with the functional information required to describe an acceptable gas state for the compartment, which can be calculated before any gas is even introduced.
Second Mistake:
The second mistake is closely related to the first mistake discussed above. It is the belief that entropy = functional information. To expose this misunderstanding, we can rearrange Eqn. (1) to get,
I(Ex) = log2(N) – log2(M(Ex)) Equation (1a)
where the first term, log2(N), represents the ground state, or the maximum Shannon entropy (or Shannon uncertainty6) the system permits when function is not required, and the second term, log2(M(Ex)), represents the Shannon entropy of the functional state of the system or sequence set.
Key observation: From Eqn. (1a) we can see that functional information represents the decrease in Shannon entropy required to achieve the desired function. In other words, the Shannon entropy of the functional state is always less than, or equal to, the Shannon entropy of the ground state.
It follows from this that if increasing the Shannon entropy to the maximum value permitted by the system still satisfies the functional requirements, then log2(N) = log2(M(Ex) and I(Ex) = 0 bits.
Bottom line: As the Shannon entropy required for functionality increases, the amount of functional information required to satisfy functionality decreases…quite the opposite of what some scientists mistakenly assert.
Summary:
Within the context of discussing functional information in biological life, it is crucial that one:
- clearly understand the distinction between classical approaches to information and the more recent, functional information as defined by Hazen et al. and,
- grasp the mathematical definition and application of functional information sufficiently well to avoid the misunderstanding that entropy = information.
Entropy does not produce functional information, at least not any statistically significant level of functional information. There is only one thing we have observed thus far that can create significant levels of functional information and digital software: intelligent minds. The fingerprints of an intelligent mind, therefore, are all over the genomes of life and it’s digital software.
References:
(1) “Craig Venter DNA: The software of Life,” Front Line Genomics, 2014.
(2) “Functional information: Molecular messages,” 2003 Nature.
(3) “Kolmogorov Complexity — A Primer”
(4) “Functional information and the emergence of biocomplexity,” 2007, PNAS.
(5) “Measuring the functional sequence complexity of proteins,” 2007, Theoretical Biology and Medical Modelling.
(6) C.E. Shannon, “A mathematical theory of communication,” 1948.
Image: Red-tailed hawk with multiple sequence alignment for a protein family, by Kirk Durston.
Cross-posted at Contemplations.
