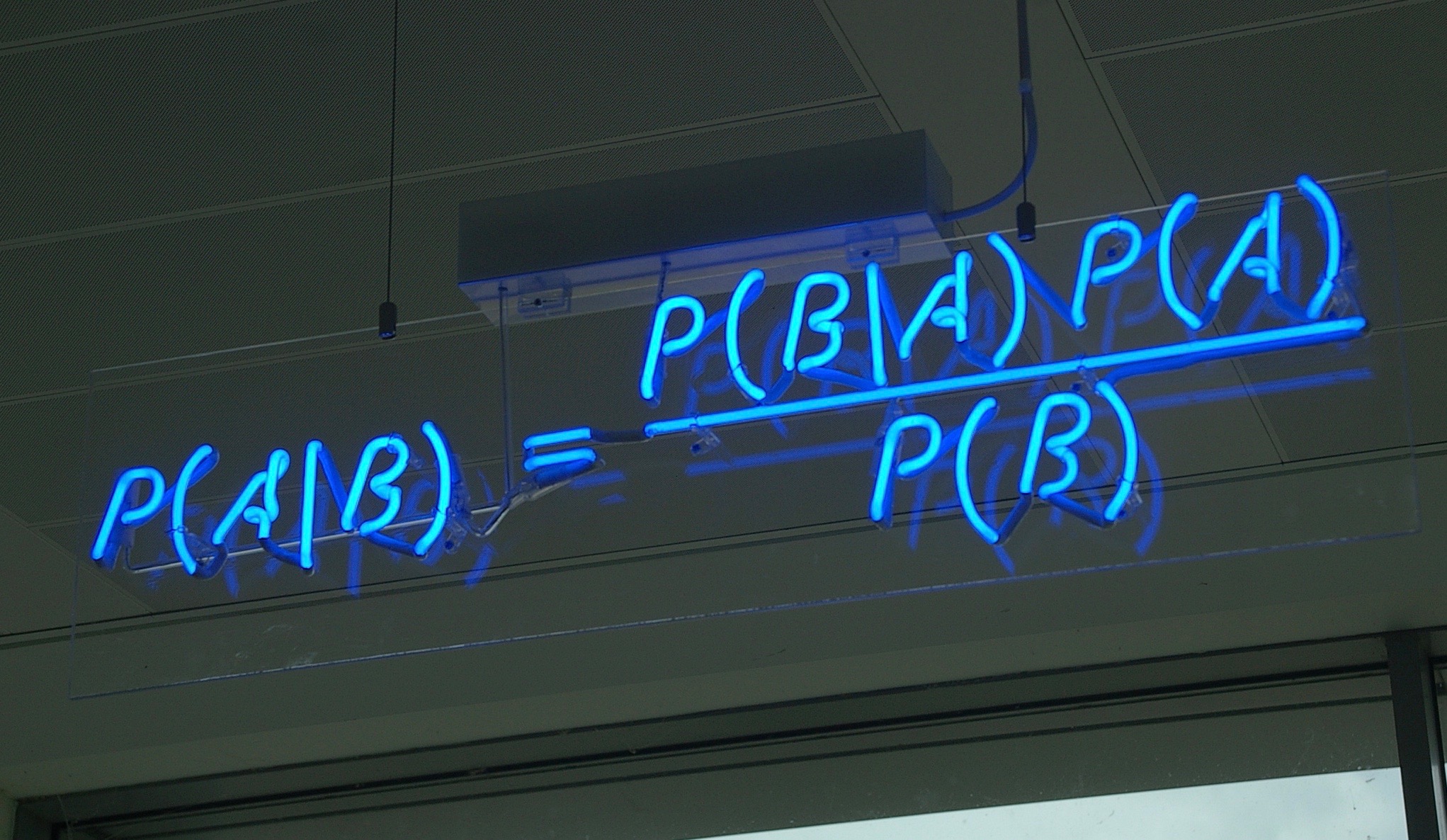
I have recently been interested in the field of epistemology, which is the branch of philosophy that deals with how we reliably form beliefs, or how we acquire knowledge. In particular, I have been interested in how we can quantify the strength of a particular piece of evidence, and how a cumulative case, involving many different lines of evidence, may be modeled mathematically. I have come to think of evidence in Bayesian terms and this has in turn impacted the way I think about the biological arguments for intelligent design.

What is Bayes’ Theorem?

Named for the 18th-century English Presbyterian minister Thomas Bayes, Bayes’ Theorem is a mathematical tool for modelling our evaluation of evidences to appropriately apportion the confidence in our conclusions to the strength of the evidence. Expressed in mathematical terms, small pieces of evidence, no single piece by itself of very great weight, can combine to create a massive cumulative case.

The strength of the evidence for a proposition is best measured in terms of the ratio of two probabilities, P(E|H) and P(E|~H) — that is, the probability of the evidence (E) given that the hypothesis (H) is true, and the probability of E given that H is false. That ratio may be top heavy (in which case E favors H), bottom heavy, or neither (in which case E favors neither hypothesis, and we would not call it evidence for or against H). Note that the probability of the evidence given your hypothesis does not need to be high for the data to count as evidence in favor of your hypothesis. Rather, the probability of the evidence only needs to be higher on the truth of the hypothesis than on its falsehood.

To take an example, suppose that P(E1|H) = 0.2, but P(E1|~H) = 0.04. Then the ratio P(E1|H)/P(E1|~H) has the value of 5 to 1, or just 5. If there are multiple pieces of independent evidence, their power accumulates exponentially. Five such pieces would yield a cumulative ratio of 3125 to 1. If the initial ratio were 2 to 1, ten pieces of independent evidence would have a cumulative power of more than 1000 to 1. 

Application to Intelligent Design

How might this way of approaching evidence relate to intelligent design? In 2004 and 2005, Lydia McGrew (a widely published analytic philosopher) and her husband Timothy McGrew (chairman of the department of philosophy at Western Michigan University) published two papers in the journals Philosophia Christi and Philo, respectively. They set out how the case for intelligent design might be formulated in terms of a Bayesian inference (McGrew, 2004; McGrew, 2005). For non-technical readers, Lydia McGrew’s Philo article is the more accessible of the two.

While other approaches to constructing the design inference (such as Stephen Meyer’s inference to the best explanation, or William Dembski’s explanatory filter, which works by elimination of the null hypothesis of chance and physical necessity) have received widespread attention within the ID community, it is, in my opinion, unfortunate that the contributions of the McGrews are seldom discussed in the current conversation, at least as far as the life sciences are concerned. Certainly, the Bayesian approach to the design hypothesis has not received anything like the same level of adoption. I believe, however, that the method they propose of articulating the case for design is worthy of serious consideration.

When it comes to the argument for design based on the physical sciences, a Bayesian approach is much more popular. Luke Barnes (a theoretical astrophysicist, cosmologist, and postdoctoral researcher at Western Sydney University), for example, employs a Bayesian approach to the question of fine-tuning of the initial parameters of our universe (Barnes, 2018). This stands in contradistinction to the deductive formulation presented by William Lane Craig, which takes the following form:

• Premise 1: Fine-tuning is due to either necessity, chance, or design.
• Premise 2: Fine-tuning is not due to either necessity or chance.
• Conclusion: Therefore, fine-tuning is due to design.

In contrast, the Bayesian formulation of the fine-tuning argument is typically presented along the following lines: Our universe shows extraordinary fine-tuning. For the cosmological constant alone the variability for life of any form to exist seems to be as low as 1 in 10¹²⁰. If it were to be modified even slightly either the universe would expand so rapidly we would only ever get the two lightest elements of hydrogen and helium, or the universe would collapse in on itself, due to gravity, within picoseconds of the Big Bang. Either way, no life could exist. 

The likelihood of unguided blind and unintelligent mechanisms producing such a precise and finely tuned feature is incredibly low. However, an intelligent agent is capable of thinking ahead with will, foresight, and intentionality to rapidly find rare and isolated solutions for the physical laws and constants that fit the requirement of a life-friendly universe. Therefore, the likelihood of an intelligent agent producing such precision in the physical laws and constants of our universe is much higher than the likelihood of blind, unintelligent mechanisms doing the same. In view, therefore, of the top-heavy ratio of P(E|H) and P(E|~H), the observation of fine-tuning counts as strong confirmatory evidence in favor of the hypothesis of cosmic intelligent design.

How can we apply this principle to the case for biological design? I will answer that question tomorrow.