 Evolution
Evolution
 Intelligent Design
Intelligent Design
A Taxonomy of Information
Note: I’ve gotten a few requests for notes or a handout from my recent talk at the Christian Scientific Society meeting, “A Taxonomy of Information and the Design Inference.” The talk should be available online eventually, but for the time being below is a condensed and reader-friendly reformatted version of my notes from the talk. The rough notes are also available here as a PDF.
The question I want to address is this: What are some common definitions of information, and which definition is most useful for making the design inference? To answer this question, let’s review several different definitions of information.
What Is Information?
Information is not always easy to define, but it often involves a measure of degree of randomness. The fundamental intuition behind information is a reduction in possibilities. The more possibilities you rule out, the more information you’ve conveyed.
Nature can produce “information” under certain definitions. Intelligent agents also produce information (certain types, at least). As Henry Quastler observed, “The creation of new information is habitually associated with conscious activity.”
To put it another way: The reduction in uncertainty could occur by an intelligent agent, or through a physical occurrence. For example:
- Nature: Blue sky reduces uncertainty about whether it is raining.
- Intelligent agents: 18 people playing baseball outdoors reduces uncertainty about whether it is raining.
Syntactic Information
Syntactic information is information that often (though not always) involves a sequence of symbols. Syntactic information uses a set of characters or symbols, or some other set of items. Symbols put into a sequence, where symbols are drawn from a fixed symbol set, with one symbol at each position.
Examples include: written language, binary code, computer language. But must syntactic information be an alphabet? Would a color count? How about a nucleotide base, like TGA?

Shannon Information
Shannon information always pertains to syntactic information, using a fixed character set, with characters in a sequence. It’s based upon the probability of a sequence occurring. Once you have that fixed character set, you can start asking about probabilities. For example, in calculating probabilities, some letters appear more than others — i.e., “e” appears 13 percent of the time, or “q” is followed by “u” nearly 100 percent of the time.
Shannon information is measured in bits. Bits = I = – Log2 (p) (where p = probability). How do you calculate in Log2? It’s easy!
- Loga (x) = Logb (x) / Logb (a)
- Loga (p) = Logb (p) / Logb (a)
- So we can calculate bits as follows: – Log2 (p) = – Log10 (p) / Log10 (2)
Here’s a little tutorial on Shannon information, using binary code as an example:
In binary code, each character has 2 possibilities: 0 or 1. Thus, the probability of any character = 0.5. So how much information does each binary digit convey? Here’s the equation:
– Log2 (0.5) = – Log10 (0.5) / Log10 (2) = 1
In binary code, each binary digit conveys 1 bit of information. Thus, a string like “00110” contains 5 bits. But here’s a key point: “5 bits” doesn’t tell you anything about the content or meaning of the string!
Shannon information is thus only concerned with reduction in uncertainty. It is not concerned with the content or “meaning” of the string. A random string might have the same Shannon information as a meaningful string. Thus, the purpose of Shannon information is to help measure fidelity of transmission of information. What the transmission says doesn’t matter.
For example, consider this 22-character string (generated by Random.org/strings):
IOAPWYDJNDGAJFLEBRSNYN
The string has 103 bits of Shannon information (using only capital letters; assuming equal probability of all letters).
Now consider this 22-character string (only upper case letters):
THISISANONRANDOMSTRING
This string likewise has 103 bits of Shannon information.
The random and non-random strings have the same amount of Shannon information! Shannon information does not help you distinguish between functional and non-functional information. Thus Shannon information doesn’t quite capture the special nature of living organisms and other designed structures:
[C]lassical information theory [i.e., Shannon information] … does not consider the meaning of a message, defining the information content of a string of symbols as simply that required to specify, store or transmit the string. … A new measure of information — functional information — is required to account for all possible sequences that could potentially carry out an equivalent biochemical function, independent of the structure or mechanism used.”
(Nobel Prize winner Jack W. Szostak, “Molecular messages,” Nature, 423: 689 (June 12, 2003).)
Kolmogorov Information
Kolmogorov complexity is a form of algorithmic information theory. Andrey Kolmogorov sought to understand randomness. His definition of information pertained to compressibility of a string, and compressibility assumes a computer environment. We can thus express Kolmogorov complexity in terms of computer programming commands. Winston Ewert’s definitions are very good: “Length of the smallest program that produces a given output” or “The number of symbols required to describe the object.”
Under Kolmogorov complexity, compressibility ~ 1/randomness. If it’s compressible, it’s NOT random (and it’s not complex). If it’s not compressible it’s random (and it’s very complex).
For example, assume we have the string 000,111,000. We could compress it to “0,1,0.” It’s highly compressible with, therefore, low Kolmogorov complexity.
How many 1-bit programs are possible? Two: 0 and 1. How many programs with 100 bits? 2100. Very few 100-bit sequences would be compressible.
As another example, consider this string:
111111111111111111111111111111111111111111111111111111111
It’s very compressible: “Repeat ‘1’ 57 times.” It has low Kolmogorov complexity.
Now consider this string (From Random.org):
4858686631031287008016234687093634769523
This one is much harder to describe, and it’s not compressible. It has much higher Kolmogorov complexity.
How about this example:
KOMOLGOROVINFORMATIONISAPOORMEASUREOFBIOLOGICALCOMPLEXITY
How might we compress it? By removing its vowels?
How about this one:
JLNNUKFPDARKSWUVWEYTYKARRBVCLTLOPDOUUMUEVCRLQTSFFWKJDXS
It’s a random string — not compressible.
Here’s the point: Kolmogorov information is not necessarily tied to likelihood. In fact, higher Kolmogorov bits could mean more randomness. In that regard, it’s not useful for distinguishing functional information from non-functional.
Semantic Information
The definition of semantic information is information that has meaning. As Dr. Randy Isaac explains, semantic information indicates “the significance of a message, whether or not an intelligent agent was involved.” (“Information, Intelligence and the Origins of Life,” PSCF 63(4):219-230 (Dec. 2011).) Is this the best way to detect design?
Well, where does meaning come from? We assign it. This is not what Shannon had in mind, and it’s really not what’s at stake with complex and specified information (CSI), as I’ll explain below.
CSI identifies some subset within a reference class of possibilities. Semantic information looks at subjective meaning. But CSI isn’t about subjective meaning. It’s objective.
Dr. Isaac writes: “In abstract symbolism, the symbol has a meaning assigned to it which does not necessarily derive from its physical properties.” I agree. Semantic information could occur by a natural cause, or by intelligence. For example:
- Human intelligence creates stop signs to tell car drivers to stop.
- Nature uses TGA in the genetic code to tell translation to stop.
In the genetic code, any other codon would serve to signify “stop.” Does TGA then possess abstract meaning assigned to it that doesn’t derive from its physical properties? Yes, it does. Why, then, should the genetic code be considered anything but intelligently designed, semantic information?
Randy Isaac further writes: “Coding in and of itself does not necessitate intelligence unless the coding represents abstract symbolic meaning,” and “Abstract symbolism is a hallmark of intelligence, especially as manifest in language and communication techniques.” Yes — I agree! So again, why should the genetic code be excluded from examples of abstract symbolism? It too carries semantic information that, presumably, we can use to detect design.
Complex and Specified Information (CSI) and the Design Inference
Complex and specified information can be understood as follows:
- Complexity is related to unlikelihood. Information is “complex” if it is unlikely.
- Specification is present if an event or string or scenario or object matches an independent pattern.
Stephen Meyer gives these examples of CSI:
Our experience-based knowledge of information-flow confirms that systems with large amounts of specified complexity (especially codes and languages) invariably originate from an intelligent source — from a mind or personal agent.
(Stephen C. Meyer, “The origin of biological information and the higher taxonomic categories,” Proceedings of the Biological Society of Washington, 117(2):213-239 (2004).)
It’s important to understand that the idea of complex and specified information is NOT an invention of ID proponents. The first use I’m aware of comes from origin-of-life theorist Leslie Orgel in the 1970s:
[L]iving organisms are distinguished by their specified complexity. Crystals are usually taken as the prototypes of simple, well-specified structures, because they consist of a very large number of identical molecules packed together in a uniform way. Lumps of granite or random mixtures of polymers are examples of structures which are complex but not specified. The crystals fail to qualify as living because they lack complexity; the mixtures of polymers fail to qualify because they lack specificity.
(Leslie E. Orgel, The Origins of Life: Molecules and Natural Selection, p. 189 (Chapman & Hall: London, 1973).)
Between CSI and Semantic Information, Which Is the Better Indicator of Design?
There are many examples where CSI helps us detect design in objects that clearly carry no semantic information. This shows that CSI is a superior method of detecting design, and we don’t need to necessarily find semantic information to detect design.
First, consider Mount Rushmore: This mountain has an unlikely shape that matches an independent pattern. We find high CSI, and detect design, without finding semantic information!
Or consider the life-friendly fine-tuning of the physical laws and constants of the universe. Here, we have very unlikely values of laws and constants that match a narrow pattern of settings that is required for life.
This is high CSI, but not semantic information.
Or consider a car engine: There’s no abstract “message” here, but there certainly is high CSI, and a designed system.
The same goes for the bacterial flagellum. It has a complex pattern that existed before we observed it, and it matches many aspects of designed systems. It has high CSI, but carries no semantic information.
I would describe the relationship between CSI and semantic information as follows:
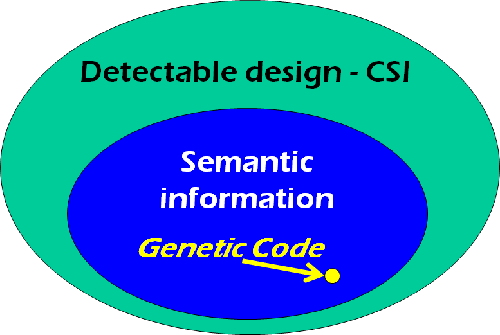
Again, semantic information is useful for detecting design — but it’s not the only way to detect design. Semantic information is a subset of CSI, which is a more generally useful definition of information for detecting design. The genetic code is a form of semantic information and is high in CSI.
Conclusion
To summarize, Information can be understood and defined in different ways. Some are useful for detecting design and/or measuring bioinformation. Some are not. Semantic information is useful for detecting design, but it’s not the only way to detect design. It’s a special case of design, not the general case. Semantic information as a class falls within complex and specified information, which is a more general mode of design detection. The genetic code is a form of syntactic, semantic, and complex specified information.

Acknowledgments:
I would like to thank William Dembski and Stephen Meyer for their insights and thoughts in preparation of this talk and material.
Image: � bozac / Dollar Photo Club.

