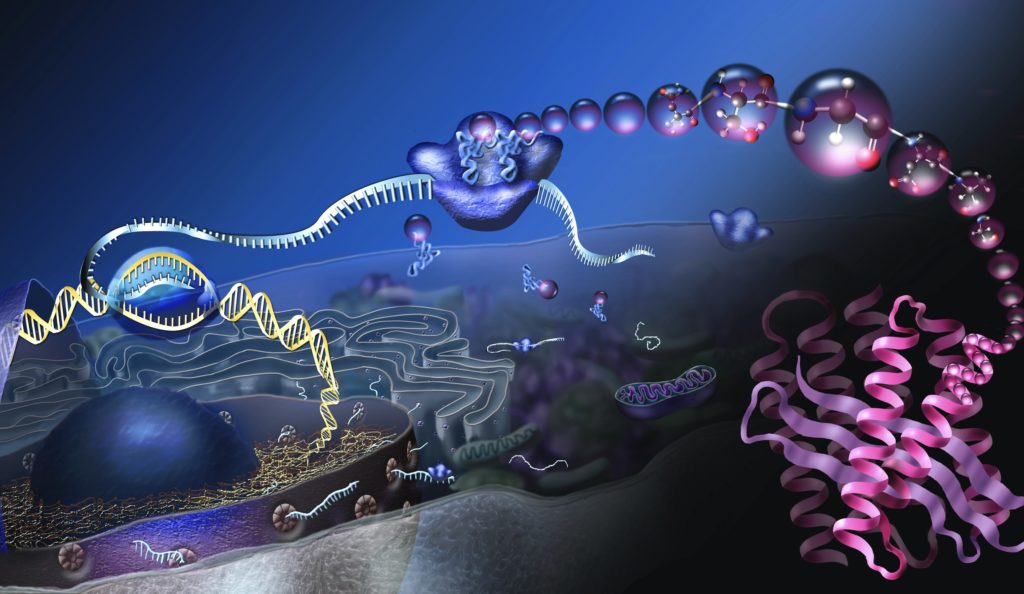
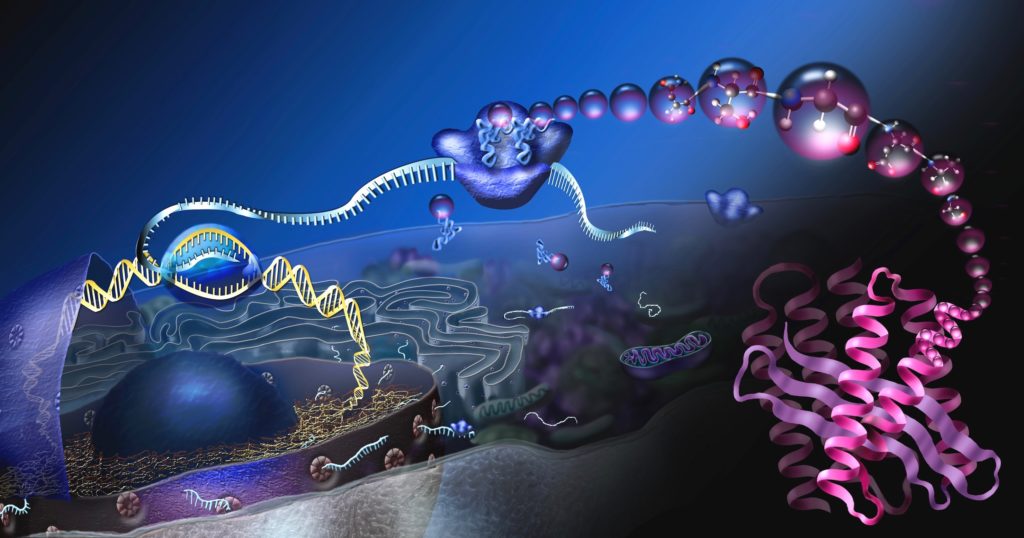
In my previous article, I provided a description of biological information and its implications for design arguments. I sacrificed on the technical details to make the content more accessible to nonexperts. Now, to provide a deeper understanding of the theoretical underpinnings of information-based arguments, I will delve into the underlying mathematics. 

Measuring Specified Complexity

One of the central requirements of design arguments is to evaluate the probability of patterns emerging through undirected processes. Examples of evaluation schema have included Behe’s irreducible complexity, Ewert et al.’s algorithmic specified complexity (ASC), and Hazen et al.’s functional information. In my previous article, I focused on the last measure. All of these approaches attempt to quantify what is termed specified complexity, which characterizes complex patterns containing meaningful (i.e., specified) information. The various approaches have been generalized by computer scientist George Montañez (see here and here). He enumerated the core steps for constructing and evaluating any measure of specified complexity:

1. Determine the probability distribution for observed events based on assumed mechanisms. In other words, identify for each possible event the probability for it to occur. 
2. Define a function that assigns to each event a specificity value. 
3. Calculate the canonical specified complexity for an outcome by taking the negative log (base 2) of the specified complexity kardis, which is the ratio of the event’s probability to its specificity value multiplied by a scaling factor. 
4. Determine the likelihood for an event to occur resulting from any proposed mechanism with the assumed probability distribution. The upper probability is equal to the kardis. If the probability is exceedingly small, the claim that the outcome occurred through the proposed mechanism can be rejected with high confidence. 

Protein Rarity

In the case of proteins, Step 1 entails modeling the probabilities for observed amino acid sequences under a uniform distribution — every sequence is assumed to be equally probable. Sequences are not actually dispersed uniformly, but this distribution serves as a neutral baseline against which to measure the difficulty of finding a functional sequence. 

Furthermore, once the uniform distribution is rejected with high confidence as an explanation, one can use the “minimum plausibility requirement” logic to determine how much more any other explanation must boost the probability of the particular outcome in order to avoid rejection as well. The required boost factor provides a quantitative way to evaluate the plausibility of evolutionary or other proposed mechanisms. This method works even if one cannot compute the full distribution for events, since one must only show that a proposed mechanism must boost the probability of the outcome by a factor of s, where s is very large. Unless the mechanism can be shown to plausibly increase the probability by that factor, it cannot be claimed as a sufficient explanation.

In addition, the uniform distribution is typically assumed if the actual distribution cannot be definitively known, as dictated by Bernoulli’s Principle of Insufficient Reason (PrOIR). 

… in the absence of any prior knowledge, we must assume that the events [in a search space] … have equal probability.

The motivation for this choice is that the uniform distribution is the least biased based on the no free lunch theorem. Consequently, selecting another probability distribution is just as likely to increase measured values or calculated probabilities as to decrease them. Moreover, no choice of distribution will dramatically increase the likelihood of highly specified events to occur unless that distribution has information about those events built into it, as mandated by the Conservation of Information dictum.   

More specifically, favorable distributions are themselves rare for each small target, and they incur their own information cost. Assuming a distribution that boosts probabilities exactly where one needs them is no more justifiable than assuming a lucky outcome (Theorem 2 in Montañez 2017 and Theorem 6 in Montañez et al. 2019). In other words, selecting a favorable distribution from the set of all possible distributions is a hard problem, so one needs an explanation for such a fortuitous choice if one wants to assume undirectedness in its selection. 

For Step 2, the protein specificity function can be chosen to assign the same value to all amino acid sequences that fold into structures that perform some biological function. That value is inversely proportional to the percentage of functional sequences. If the specificity value equals the exponential of the negative conditional Kolmogorov complexity, the canonical specified complexity reduces to the algorithmic specified complexity (Montañez 2018, p. 9). The resulting complexity measure (Step 3) takes on a value sufficiently high to reject any possibility for a randomly chosen sequence to correspond to a functional protein (Step 4), which makes the undirected evolution of many novel proteins highly implausible. 

Mutual Information

Another core concept in information theory is what is defined as the mutual information between two random variables X₁ and X₂. Each variable represents a set of outcomes of the same or varying probabilities. The mutual information quantifies to what extent knowledge of one variable provides knowledge of, or reduces uncertainty in, the second variable. 

For instance, each variable could represent a student’s response to two True/False questions on a test. Since four outcomes are equally probable (TT, TF, FT, FF), the information associated with knowing a student’s two answers is log (base 2) of 4, which is 2 bits. If at least one student randomly guessed the answer for both questions, knowing one student’s answers would provide no information about those of the second student. In contrast, if one student copied both answers from the other, knowing one student’s answers provides complete information about the second’s answers. The mutual information in the former case would then be 0 bits and in the latter case 2 bits. If one student copied one answer but guessed on the other, the mutual information would be 1 bit. The stronger the connection between the two variables, the greater the mutual information. 

In my previous article, I referenced two theorems related to the conservation of information that challenge evolutionary assumptions, and they are both based on mutual information. Space did not permit me to further develop the argument, which would have required addressing probability distributions rather than individual sequences. But, research in biological thermodynamics has rigorously demonstrated the centrality of mutual information in understanding biological systems, and the conclusions strongly reinforce design arguments, particularly in relation to the origin of life.  

Information and Entropy Reduction

Chemical and biomolecular engineer Yaşar Demire has demonstrated that the reduction in entropy in a cell requires that the mutual information between a static system Y and a dynamic system X must increase. System Y represents those cellular structures that encode the schematics for system X, and system X represents the encoded biological structures such as enzymes, molecular machines, and cell membranes. The most obvious information repository in system Y is DNA, but other information-bearing structures would also be included. 

The increase in the mutual information corresponds to the cell processing the information in Y to direct the new structures’ construction, assembly, and installation. The classic example is a genetic sequence leading the manufacture of a protein. The emerging protein represents the creation of functional information that coincides with an increase in the mutual information with the DNA sequence. 

Demire designates the information that directs the process as “control information”

…“control information” is defined as the capacity to control the acquisition, disposition, and utilization of matter, energy, and information flows functionally. 

He goes even further by stating that the production of chemical energy coupled to the processing of information is essential for creating and maintaining a cell’s low-entropy state:

The ATP synthesis, in turn, is matched and synchronized to cellular ATP utilization processes, since energy and matter flows must be directed by the information for them to be functional and serve a purpose. For living systems, the information is the cause and the entropy reduction is the result:

Energy + Matter + Information → Locally reduced entropy (Increase of order)

He perfectly reiterates the core argument in my recent exchange with Jeremy England that the reduction in entropy entailed in the origin of life requires preexisting energy production machinery and information (see here and here). 

Image: Where proteins come from, by Nicolle Rager, National Science Foundation / Public domain.